Eletromagnetismo no Ensino Médio

Introdução

O espelho esférico é um dos temas a ser abordado em continuidade ao assunto espelhos planos, verificando algumas propriedades do comportamento da luz, como as leis da reflexão. O experimento que vamos descrever utiliza-se de um dispositivo que simula o comportamento de espelhos esféricos e parabólicos. É importante perceber que o material utilizado é de simples construção e, portanto é mais acessível do que um espelho curvo propriamente dito, além de mais barato. Devemos notar que o material se comporta como um espelho aproximadamente parabólico. No planejamento de um curso de Óptica, esta atividade pode ser utilizada por alunos que já tenham estudado espelhos planos e já tenham clareza sobre as leis da reflexão.

Objetivos

• Estudar o comportamento da luz quando incide em superfícies curvas e espelhadas;
• Verificar a validade das leis da reflexão em superfícies curvas;
• Determinar as características específicas de espelhos curvos.

Material utilizado

Placa de madeira com suportes fixos (600mmx300mm);
Chapa de aço inox com uma das faces polida (586mmx84mm);
Ponteira laser ou caixa de fenda;
Régua; Transferidor;
Compasso; Papel sulfite.

Realização do experimento

• Conhecendo os materiais: O professor posiciona a lâmina sobre a placa (sob a lâmina deve haver uma folha de sulfite para marcações posteriores) e convida os alunos a manipular o laser sobre a superfície. Neste momento, o aluno deve ser deixado livre para experimentar, sem interferência do professor. O aluno está se familiarizando com o material;

• Retomando conhecimentos sobre a reflexão: O professor propõe a seguinte atividade: o aluno deve incidir o laser no plano do papel em direção à placa e observar o raio incidente e o raio refletido sobre o papel. A seguir o aluno marcará a posição de alguns raios (quatro é um bom número) incidentes e seus respectivos raios refletidos e verificará a validade ou não das leis da reflexão nessa superfície curva. Para tanto, o aluno deverá marcar um ponto sobre o raio incidente, um ponto sobre o raio refletido, o ponto de incidência na lâmina e a curva da lâmina neste trecho. Essas marcações serão feitas no papel. Após essas marcações o aluno deverá retirar o papel, traçar os raios (ligando o ponto de incidência com cada um dos pontos encontrados), e determinar uma reta perpendicular à lâmina no ponto de incidência, essa reta é a normal e é a partir dela que o aluno determinará os ângulos de incidência e de reflexão conforme estudado em espelhos planos. O professor poderá organizar os dados obtidos pelos alunos em uma tabela para análise dos mesmos pela classe toda.

• Determinação da normal no ponto de incidência: Esta pode ser uma dificuldade e é o momento para o professor orientar a solução de um problema de Geometria. Para traçar a reta normal no ponto de incidência o aluno precisará de uma régua e um compasso:
•  Com a ponta seca do compasso sobre o ponto P de incidência, faça uma abertura pequena (2 a 3 cm) e trace dois pontos sobre a curva do espelho:

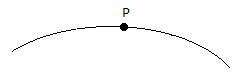
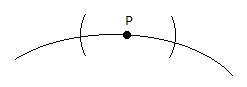
•  Chamaremos esses dois novos pontos de X e Y:

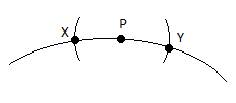
•  Com a ponta seca do compasso sobre o ponto X e uma abertura um pouco maior que a distância entre X e P, trace duas curvas em lados opostos ao ponto P. Mantendo a mesma a abertura e com a ponta seca em Y trace duas curvas que interceptem as curvas traçadas anteriormente:
•  Agora basta traçar a normal unindo os pontos encontrados e voltar para o problema da reflexão da luz e suas leis, fazendo as medições adequadas para vários pontos P.

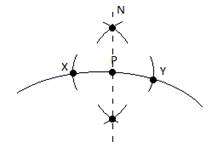
• Procurando um particular ponto de “convergência”: nesse momento é possível orientar o procedimento experimental para chegar à caracterização dos elementos principais dos espelhos curvos, particularmente os parabólicos. O professor agora deverá posicionar uma nova folha de sulfite sob a lâmina e traçar uma reta ligando as extremidades da lâmina. A seguir, o aluno deverá utilizar o laser para incidir a luz na lâmina perpendicularmente a esta reta. O aluno deverá percorrer toda a lâmina e observar o que acontece, sempre se mantendo perpendicular. O aluno perceberá que todos os raios incidentes e paralelos serão refletidos tendendo a uma mesma região do papel (uma região central). O professor neste momento poderá apontar para a existência de um “ponto” (uma pequena região) de intersecção de todos esses raios refletidos. O aluno poderá determinar esse ponto de convergência dos raios e testar essa posição para outros raios incidentes. Esse “ponto” é o Foco do espelho. Este é um importante elemento geométrico do espelho curvo, determinado experimentalmente. 

• Delimitando a área de atuação: se os alunos não perceberem que esse ponto (Foco) existe para uma região “central” da superfície, o professor poderá orientá-los a observar essa região específica e discutir a curvatura da lâmina, que nas extremidades tende a ficar plana. De fato, ela não é esférica e nem exatamente parabólica, trata-se de uma aproximação.

• Determinando o Centro de Curvatura do espelho: o aluno deverá agora traçar o centro geométrico do espelho curvo no plano do papel. Para isso, o aluno deverá posicionar outra folha sulfite sob a lâmina, traçar sobre ela a curvatura do espelho e determinar esse ponto central. Para tanto o aluno deverá traçar um segmento ligando os dois pontos nas extremidades do espelho, determinar o ponto médio desse segmento e traçar a reta perpendicular a esse segmento no ponto médio. A intersecção desta reta com o traçado do espelho será o Vértice do espelho. Essa reta perpendicular, teoricamente, contém o Foco. Como nosso espelho não é perfeitamente parabólico nem esférico, isso poderá não ocorrer. De qualquer modo, vamos considerar uma aproximação para o Centro de Curvatura do espelho como o dobro da distância entre o Vértice e o Foco. 

• Conhecendo a parte externa da superfície lisa e curva: o aluno trabalhou até o momento com a parte interna da superfície esférica (côncava), mas poderá aplicar os mesmos procedimentos para verificar o comportamento do raio de luz na parte externa (convexa) da lâmina, porém fazendo o prolongamento de todos os segmentos encontrados para observar os mesmos elementos determinados da parte interna da lâmina espelhada.

• Observando o comportamento da luz em casos específicos: os casos específicos permitem a caracterização das propriedades dos espelhos esféricos de Gauss. Consideramos espelho esférico de Gauss aquele de pequena abertura, o que não conjuga de um ponto luminoso uma mancha e sim uma imagem nítida. Podemos considerar que as condições de Gauss são satisfeitas em uma região central do nosso espelho (com um ângulo de abertura de aproximadamente 5°)

 Conclusões

•  Os alunos perceberão que as leis da reflexão estudadas para espelhos planos continuam válidas em espelhos curvos;
•  Realizando um experimento como esse o aluno tem oportunidade de fazer observações e explorar o comportamento do raio de luz numa superfície lisa curva;
•  Esse material oferece condições para realizar o experimento, mas, com certas limitações. Devemos verificar que as laterais dessa superfície curva têm praticamente comportamento de espelhos planos;
•  O aluno tem condições de perceber que existe um padrão de comportamento do raio de luz, que leva a convergência num determinado ponto. Isso ocorre porque, em um espelho esférico as normais em cada ponto são coincidentes com os raios da circunferência, que se encontram no centro da mesma. Como o raio refletido é simétrico ao raio incidente, em relação à normal, quando incidimos, por exemplo, do lado esquerdo do espelho (à esquerda da normal), o raio refletido ficará do lado direito da normal e, analogamente, quando incidimos do lado direito, o raio refletido ficará do lado esquerdo, fazendo com que todos os raios refletidos tendam a uma região central. Pela lei da reversibilidade, se pensarmos nos raios incidentes em sentidos contrários, os refletidos tenderão a divergir. Nosso espelho não é esférico, mas tem comportamento semelhante, pois se aproxima de uma superfície esférica;
•  É fácil verificar a simetria existente nesse elemento esférico através do comportamento do raio de luz;
•  Todo procedimento adotado nesse experimento poderá levar o aluno a construir os elementos necessários para entender todo o formalismo utilizado no estudo dos espelhos esféricos;
•  Na realização do experimento a matemática aparece como suporte importante para encontrar os elementos geométricos da superfície esférica.

PSSC. Física – parte 2, p. 35-36. EDART. São Paulo.
Alvarenga, Beatriz e Máximo, Antônio. Física – vol. 2. Ed. Bernardo Álvares SA. 1970.