|
Vamos
utilizar uma análise similar à anteriormente realizada para
a fenda estreita na aproximação de Fraunhofer para
entendermos o funcionamento da rede de difração mostrada na
Fig. 9.16. Começaremos com a expressão dada pela eq. (9.19)
e somaremos para as várias fendas paralelas. Assim
temos: 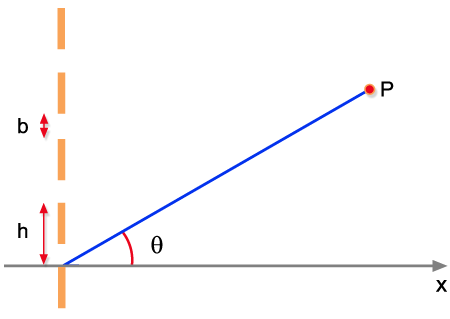 Fig. 9.16 - Rede de difração.
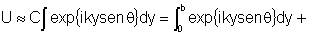 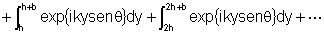
onde o número de integrais do lado direto é igual ao
número de fendas paralelas, que tomaremos como 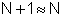 , para N>>1. Esta expressão pode ser escrita da forma: , para N>>1. Esta expressão pode ser escrita da forma: 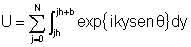 para N+1 fendas. Assim, realizando a integração temos: 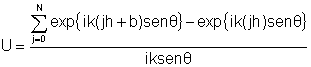 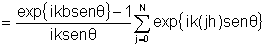
Desta expressão é possível mostrar, embora não o façamos aqui, que 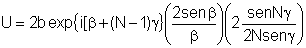 onde 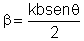 e e 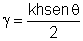 . Logo, . Logo,
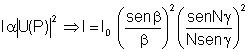
com  sendo o fator de difração e sendo o fator de difração e 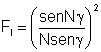 o fator de interferência. A Fig. 9.17 mostra o padrão de
difração e interferência para a rede considerada. Vemos que
FD = 0 para
o fator de interferência. A Fig. 9.17 mostra o padrão de
difração e interferência para a rede considerada. Vemos que
FD = 0 para 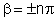 (n = inteiro diferente de zero) e FD é máximo para (n = inteiro diferente de zero) e FD é máximo para 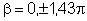 , etc. Por outro lado, FI = 0 quando , etc. Por outro lado, FI = 0 quando 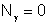 , ou seja, quando , ou seja, quando 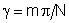 , e máximo para , e máximo para 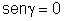 , o que implica em , o que implica em 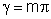 e consequentemente, e consequentemente, 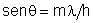 . . 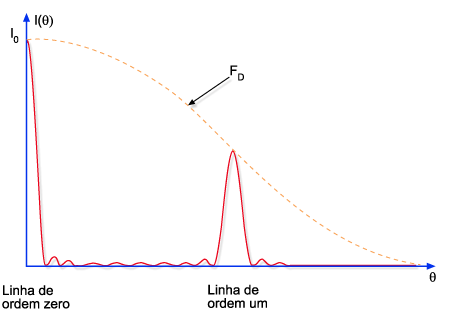
Fig. 9.17 - I(q) para uma rede de difração.
O poder de resolução da rede de difração é definido como 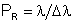 , onde , onde 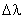 é a separação entre duas linhas espectrais, que pode ser
obtida usando-se o critério de Rayleigh, mostrado na
Fig. 9.18. Este critério estabelece que duas linhas
estarão resolvidas quando o máximo de uma coincide com o
zero da outra. A dispersão angular de uma rede é dada por
é a separação entre duas linhas espectrais, que pode ser
obtida usando-se o critério de Rayleigh, mostrado na
Fig. 9.18. Este critério estabelece que duas linhas
estarão resolvidas quando o máximo de uma coincide com o
zero da outra. A dispersão angular de uma rede é dada por 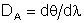 , mas como (condição de máximo de FI), temos que , mas como (condição de máximo de FI), temos que 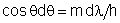 e portanto e portanto 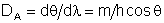 . Por outro lado, . Por outro lado,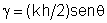 e assim e assim 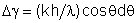 . Do critério de Rayleigh temos que . Do critério de Rayleigh temos que 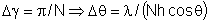 . Como obtemos . Como obtemos  e portanto o poder de resolução da rede é: e portanto o poder de resolução da rede é: 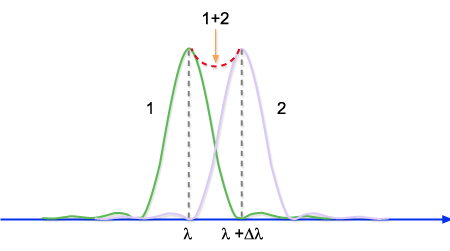 Fig. 9.18 - Critério de Rayleigh.
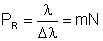
| 

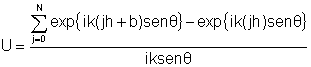
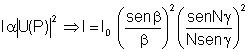
 sendo o fator de difração e
sendo o fator de difração e 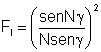 o fator de interferência. A Fig. 9.17 mostra o padrão de
difração e interferência para a rede considerada. Vemos que
FD = 0 para
o fator de interferência. A Fig. 9.17 mostra o padrão de
difração e interferência para a rede considerada. Vemos que
FD = 0 para 

