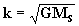Cálculo das Órbitas Planetárias
por Eng. Andrés Esteban de la Plaza
ÍNDICE:
REPRESENTAÇÃO DE VETORES.
ACELERAÇÃO EM COORDENADAS POLARES.
FORÇAS CENTRAIS E GRAVITAÇÃO.
RESOLUÇÃO DE EQUAÇÃO DIFERENCIAL DO PROBLEMA.
CONSIDERAÇÕES PARA AS ÓRBITAS ELÍPTICAS.
CÁLCULO DA POSIÇÃO NA ÓRBITA ELÍPTICA.
CONSIDERAÇÕES SOBRE :
CÁLCULO DE ÓRBITAS NÃO ELÍPTICAS:
1.
REPRESENTAÇÃO DE VETORES
A posição de um ponto P
no espaço pode ser definida por um vetor posição
 com origem num centro O de coordenadas ortogonais retangulares.
Definindo nesta terna xyz,
os versores (vetores unitários) dos eixos, obtemos
respectivamente : o versor
com origem num centro O de coordenadas ortogonais retangulares.
Definindo nesta terna xyz,
os versores (vetores unitários) dos eixos, obtemos
respectivamente : o versor  como versor da
direção x, o versor
como versor da
direção x, o versor  como o versor da direção y, e o versor
como o versor da direção y, e o versor
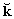 como o versor da direção z.
Assim, qualquer vetor definido num destes eixos estará representado pelo produto
de um escalar igual ao módulo e do versor da direção
como o versor da direção z.
Assim, qualquer vetor definido num destes eixos estará representado pelo produto
de um escalar igual ao módulo e do versor da direção
Þ  .
.

Portanto, podemos decompor o vetor
 em seus componentes ortogonais
em seus componentes ortogonais
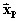 ,
, 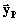 e
e
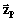 no sistema de centro O:
( projeções de
no sistema de centro O:
( projeções de  nos eixos x, y, e z ) de forma que
nos eixos x, y, e z ) de forma que
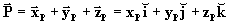 .
Também podemos representar este vetor de forma matricial:
.
Também podemos representar este vetor de forma matricial:

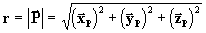
Porém esta não é única
representação possível para o ponto P. Podemos imaginar um
plano que contém o vetor  e o centro O, de maneira que, embora ainda continuemos no
espaço tridimensional, a representação de
e o centro O, de maneira que, embora ainda continuemos no
espaço tridimensional, a representação de
 é feita num plano,
entretanto, este plano será um plano complexo ou seja, o eixo x
será real, e o eixo y será imaginário, ou seja:
é feita num plano,
entretanto, este plano será um plano complexo ou seja, o eixo x
será real, e o eixo y será imaginário, ou seja:

A vantagem de procedermos assim está dada pela possibilidade
de representarmos um número complexo na sua forma exponencial, como um vetor. Ë
fácil observar que se definimos o versor  para a direção x, então a direção de r
estará definida por um versor
para a direção x, então a direção de r
estará definida por um versor  tal que
tal que
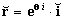 onde
onde  , logo:
, logo:

de forma que:
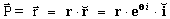
que é a expressão do raio vetor em coordenadas polares.
2. ACELERAÇÃO EM COORDENADAS POLARES
Podemos agora proceder a derivar
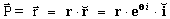 respeito de tempo para
encontrar a aceleração. Porém antes vamos calcular a derivada
respeito do tempo de
respeito de tempo para
encontrar a aceleração. Porém antes vamos calcular a derivada
respeito do tempo de  , pois é
uma função de q, ou seja que
, pois é
uma função de q, ou seja que
 =
=
 (q):
(q):

vamos calcular então a primeira derivada de
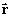 , ou seja
, ou seja
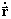 :
:
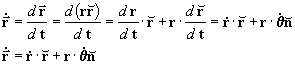
vamos calcular agora a segunda derivada de
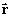 , ou seja
, ou seja
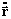 :
:
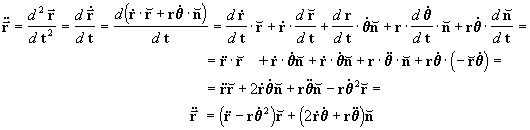

onde:

3.
FORÇAS CENTRAIS E GRAVITAÇÃO
Inicialmente vamos deduzir as fórmulas que determinam as trajetórias
dos corpos que se encontram sujeitos à atração de forças
centrais, no caso particular da a lei da gravitação universal, ou seja
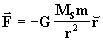 .
.
De acordo com a figura 1 temos:
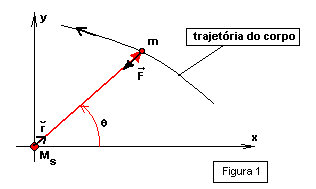
Onde o ponto m está submetido
à força :

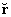 é o versor (vetor unitário)
da direção de
é o versor (vetor unitário)
da direção de
 e:
e:
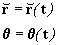
t = tempo
MS = massa corpo central m = massa objeto
A resolução deste problema deve proporcionar as
seguintes funções:

As expressões para a aceleração em
função das componentes normal e radial da
aceleração são:
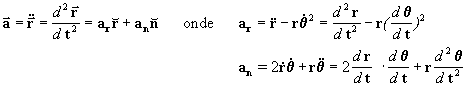
Mas nos sistemas de forças centrais sabemos que a
aceleração normal é nula Þ
an=0, portanto a aceleração será:
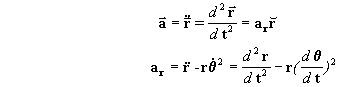
e lembrando que a equação diferencial
geral do movimento central neste caso é:
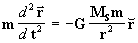
4. RESOLUÇÃO DA EQUAÇÃO DIFERENCIAL DO
PROBLEMA
A equação diferencial geral do problema pode ser decomposta em
duas particulares:
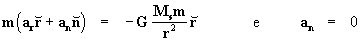
temos então:
mar = 
man= 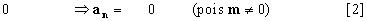
então a equação diferencial
que temos que resolver será:
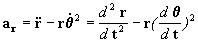
[1]
porém não conhecemos as relações
 , mas lembrando da equaçã
o [2] obtemos que:
, mas lembrando da equaçã
o [2] obtemos que:
an = 0
Þ

ou seja

 entretanto
entretanto
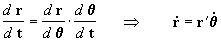
De
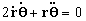 podemos obter
podemos obter
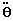 , ou seja:
, ou seja:
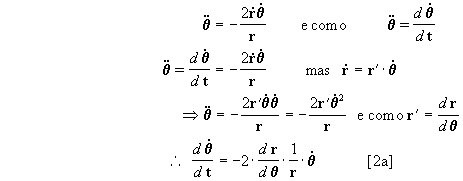
fazendo passagem de términos na [2 a] obtemos:

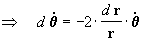

integrando agora a [3]:
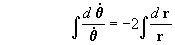
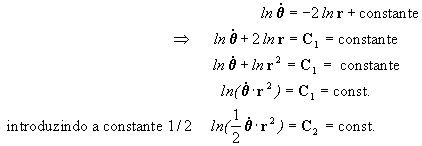
portanto Þ
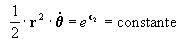
que não é outra coisa senão
a velocidade areolar do ponto m na sua trajetória, como podemos observar
na figura 2:

- Se a velocidade areolar é constante, então:
"os planetas varrem áreas iguais em tempos
iguais" .
A área do
triângulo será:
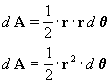
Vamos fazer agora algumas considerações energéticas. Para
isto definimos:

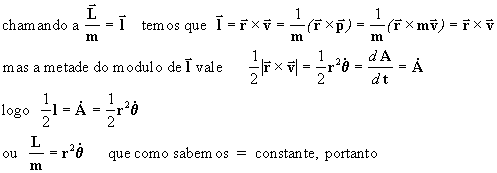

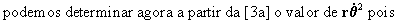
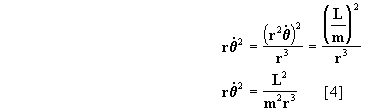
Logo, para resolver a equação diferencial [1] , já temos o valor
 porém falta conhecermos o valor de
porém falta conhecermos o valor de
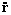 . Para isto, e voltando agora
à aceleração radial:
. Para isto, e voltando agora
à aceleração radial:

observamos que
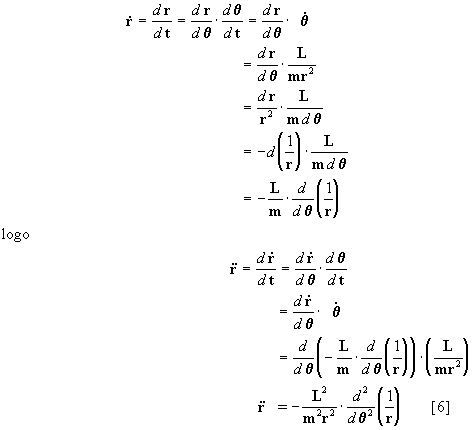
Agora, substituímos [6] e [4] na eq.
diferencial [5] e obtemos então:
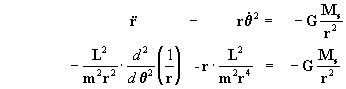
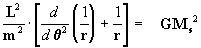
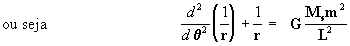
Fazendo 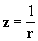 e
substituindo, chegamos a uma equação diferencial [7] de
fácil resolução:
e
substituindo, chegamos a uma equação diferencial [7] de
fácil resolução:
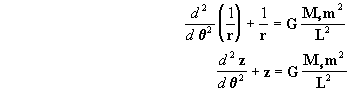
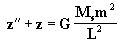
[7]
A solução geral da equação [7] compõe-se de
duas soluções; a solução homogênea
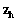 que provém de resolver
que provém de resolver
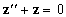 , e a solução particular
, e a solução particular
 .
.
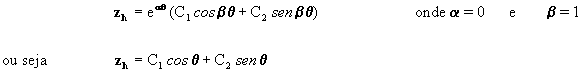
introduzindo agora as constantes
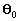 e
e
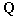 de forma que:
de forma que:
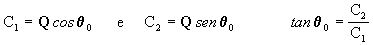
chegamos a


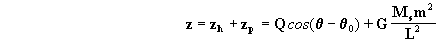
de forma que
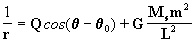
operando chegamos a
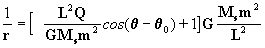
ou seja
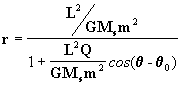
[8]
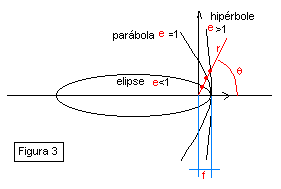
que obviamente corresponde à equação de
uma cônica (Figura 3), cuja fórmula geral é:
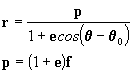 [8aa]
[8aa]
ou seja que:
 [8 a]
[8 a]
5. CONSIDERAÇÕES PARA
AS ÓRBITAS ELÍPTICAS
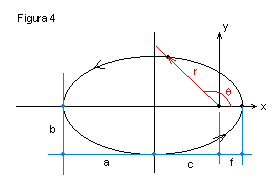
Os parâmetros da
elipse na Figura 4 são:
a: semi-eixo maior
b: semi-eixo menor
c=a2-b2
e: excentricidade = c/a
f: distância focal =
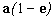
A: área da elipse =
pab=

T: período para uma revolução
|
A equação da elipse em coordenadas cartesianas é:
|
A equação da elipse em coordenadas polares é:
|
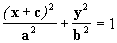 |
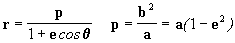 |
A velocidade com que o raio vetor r varre a área da órbita vale:
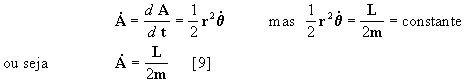
se agora integramos a [9] no tempo T
obteremos a superfície total A:
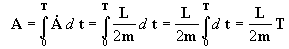
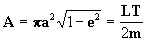
agora vamos isolar T:
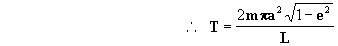
agora vamos a calcular T2 lembrando que
 , ou seja:
, ou seja:
 [10]
[10]
porém para o sistema solar, Ms=massa solar,
a=distância média do planeta ao sol, T=seu período de
revolução. Olhando a eq. [10] é óbvio que a quantidade
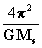 é uma constante para todos os
planetas do sistema solar. Assim temos que
é uma constante para todos os
planetas do sistema solar. Assim temos que 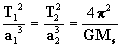 onde os subíndices 1,2, representam os diferentes planetas.
Tal é a 3a. Lei de Kepler: "Os quadrados dos períodos
de revolução dos planetas são inversamente proporcionais às
distâncias medias do sol".
onde os subíndices 1,2, representam os diferentes planetas.
Tal é a 3a. Lei de Kepler: "Os quadrados dos períodos
de revolução dos planetas são inversamente proporcionais às
distâncias medias do sol".
6. CÁLCULO
DA POSIÇÃO NA ÓRBITA ELÍPTICA
Até agora
descobrimos a função r=r(q),
de forma que sabemos qual será o tipo de curva descrita pelo ponto m
porém, falta conhecermos qual a função que determina as
variações de q em função
do tempo t, isto é, a função q
=q(t). Vamos desvendar o mistério...
Sabemos que para a elipse, em coordenadas polares, a posição do ponto
de massa m está definida pela relação r(
q
), porém não conhecemos a dependência dos parâmetros r
e q em função do tempo t.
Vamos deduzi-las então:
a velocidade areolar é:
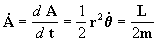
portanto, após ter descrito um ângulo
q na trajetória, em um tempo t, o
ponto m terá varrido a área A
q que será a resultante de integrarmos:
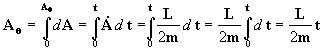
porém para termos os limites de integração
em função de q :
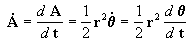
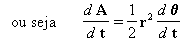
e eliminando
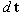 :
:
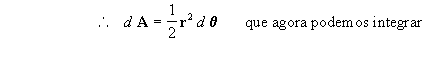
portanto 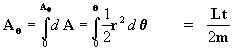 [11]
[11]
Substituindo
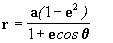 na integral acima e
multiplicando por 2, temos:
na integral acima e
multiplicando por 2, temos:
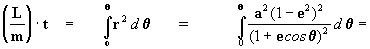
então
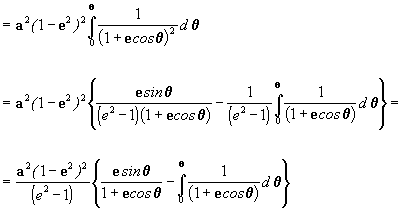
porém para a elipse Þ
e < 1 Þ
e2 < 1 logo a solução da
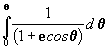 será:
será:
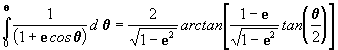
logo
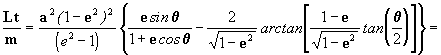
 [12]
[12]
Esta fórmula é
muito bonita porém, o resultado obtido é o inverso que
desejávamos, na verdade nós queríamos q
=q
(t) e acabamos obtendo t=f(q
). É fácil observar que despejar q
nos leva a uma equação muito complexa, ou seja, devemos encontrar outro
método.
Introduzimos agora uma
quantidade auxiliar E denominada anomalia excêntrica, que
cumpre
a seguinte condição:
 [12a]
[12a]
que eqüivale a dizer que
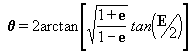
então introduzindo a [12a] na [12], temos:
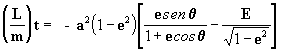 [13]
[13]
entretanto se pode demonstrar que para a quantidade auxiliar E
introduzida:
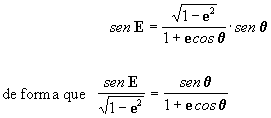
substituindo esta última na [13] chegamos a:
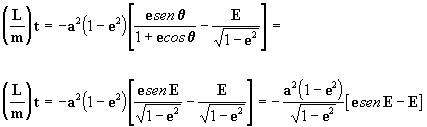
logo
 [14]
[14]
- Vamos definir agora as constantes para o cálculo prático, como:
 [15]
[15]
para o planeta Terra Þ
T=Tt e at= 1 ua (unidade
astronômica),
Þ
logo para um planeta qualquer com T, a, temos (aplicando [10]) que:
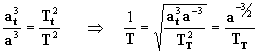 [16]
[16]
e substituindo a [16] na [15] obtemos: 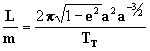
ou seja que a [14] fica:
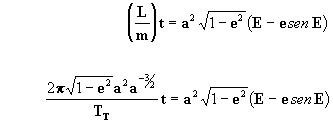
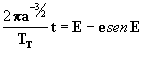 [17]
[17]
Esta última fórmula é básica, pois é a empregada
no cálculo das efemérides.
As seguintes denominações são as usuais:
q
= anomalia verdadeira [radianos] =
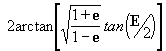 [18]
[18]
E = anomalia excêntrica =
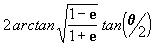 [radianos]
[radianos]
a = distancia média ao sol [ua]
(unidades astronômicas)
n = movimento diurno médio =

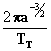 [radianos/dia]
[radianos/dia]
n = k
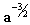 onde k=constante de Gauss =
onde k=constante de Gauss =
 [18a]
[18a]
M = anomalia média =
n Dt [19]

logo as fórmulas reduzem-se a:
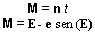
sendo t = tempo após passo pelo periélio, em dias.
TT = ano trópico = 365.256374 dias
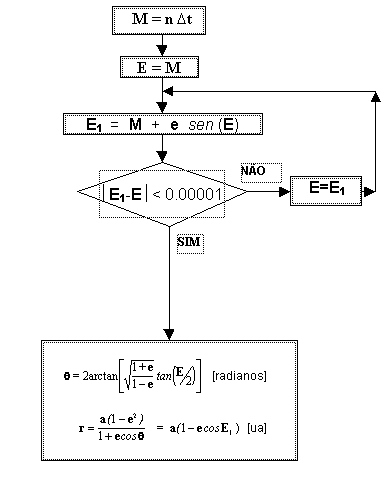
O processo
de cálculo se reduz a determinar a anomalia média M [19], e de
posse desta procedermos a calcular a anomalia excêntrica E que satisfaz
a equação de Kepler [20], logo calculamos q
segundo a [18]. Com q calculamos r ,
o que determina a posição do ponto m na órbita. A
resolução da Equação de Kepler é realizada por
iterações sucessivas, de forma que o algoritmo de cálculo é o seguinte:
D
t=T-T0 onde T0 e a data da última passagem pelo
periélio
a = distância média ao sol
Nota: Normalmente o
tempo da passagem T0 está dado em dias Julianos JD,
de forma que a data de calcula também está em dias julianos e o
cálculo de D
t se reduz apenas a encontrar a diferença (em dias julianos) entre T e
T0.
O diagrama de fluxo do algoritmo é:

Vamos fazer um exemplo de aplicação:
caso Júpiter
a = 5.208174 ua ; e = 0.049284
T = 2450896.510556 dj =24 Março 1998
T0 = 2446966.84378 dj =24 Junho 1987 (periélio)
D
t = 3929.666776 dj
n = 0.00144728573606
M = n D
t = 5.687350672374 radianos ( =325°.861190138)
E=M= 5.687350672374
E1=M+e senE= 5.659692503366
E1-E= -0.0276581690088
E=E1= 5.659692503366
E1=M+e senE=5.658575010
E1-E=-0.001117493
E=E1=5.658575010
E1=M+e senE=5.658530316
E1-E=-0.000044694
E=E1=5.688530316
E1=M+e senE=5.658528529
E1-E=-0.000001787
E=E1=5.658528529
e como senE =
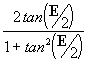 =-0.584818898 Þ
<0 Þ estamos no IV quadrante!
=-0.584818898 Þ
<0 Þ estamos no IV quadrante!
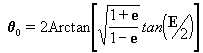 = -0.654082984
= -0.654082984
q
= 2p + q
0 = 2p
+ (-0.654082984) = 5.629102324 radianos = 322°
.5238
logo
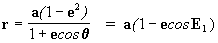 = 4.999964739 ua
= 4.999964739 ua
Segundo a efemérides,
para a data 24/03/1998, a anomalia média vale 325°
33¢35 ²
, a distância ao sol é 5.00079 ua. Comparando com nossos valores,
nossa anomalia média foi 325°
51¢40²
, e a distância 4.999964739 ua (uma diferença de 0.016%). Vale a pena
lembrar que na data da passagem pelo periélio existia uma imprecisão
quanto a hora, se a tivéssemos sabido, a diferença seria ainda menor!
Também, se considerarmos que Júpiter dá uma volta em 11.86 anos,
desde o periélio até a data de cálculo passaram-se 10.758 anos,
ou seja um pouquinho menos de 1 revolução, o que concorda com nossos
cálculos.
Após conhecermos a posição na órbita,
e sabendo os parâmetros orbitais (i:
inclinação da órbita respeito da eclíptica,
W
: longitude do nodo ascendente e w
: argumento do periélio) podemos passar das coordenadas polares para as
retangulares (coordenadas heliocêntricas orbitais), para as
heliocêntricas eclípticas, e conhecendo a posição da
Terra (em coordenadas heliocêntricas eclípticas, a diferença
nos dá o vetor Terra-Júpiter, ou seja as coordenadas geocêntricas
eclípticas de Júpiter, então apenas falta uma última
passagem, para as coordenadas geocêntricas equatoriais ( r:
distância Terra-Júpiter , a:
ascensão reta, d: declinação).
Tais cálculos efetuam-se empregando matrizes e análise vetorial
(fórmulas de Euler).
Para facilitar o cômputo da anomalia verdadeira e a
determinação do quadrante em questão, talvez resulte mais
útil o emprego das seguintes fórmulas, lembrando que a
fórmula:
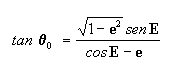 retorna o argumento q
no seu valor principal, ou seja q
0, no I e IV quadrantes.
retorna o argumento q
no seu valor principal, ou seja q
0, no I e IV quadrantes.
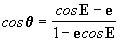
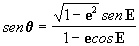
Assim:
cosq = 0
sen q > 0 q
= q0Þ
q
0 = 90°
cosq
= 0 sen q < 0
q = q
0Þq
0 = 270°
cosq
> 0 sen q
> 0 q = q
0Þq
0 > 0° 0
°
< q < 90°
cosq
< 0 sen q > 0
q = 180°
+ q0 Þ
q
0 < 0°
90° < q
< 180°
cosq
< 0 sen q < 0
q = 180°
+ q0Þ
q
0 > 0° 180
° < q
< 270°
cos
q > 0 sen
q < 0 q
= 360° + q
0 Þq
0 < 0° 270
°
< q < 360°
Também, na hora dos
cálculos, devemos observar o seguinte:
- O movimento diurno médio n = k a-1.5
pode ser expressado tanto em [ radianos / dia ] como em [
° / dia]. Ou seja, a constante de Gauss k, pode
ser expressada em:
k = 2p
/ 365.2564 [ radianos / dia ]
k = 360°
/ 365.2564 [ °
/ dia ]
- A anomalia média M = n
Dt poderá então estar expressada
em [ radianos ] ou [ ° ]. Normalmente as tabelas
ou efemérides proporcionam M em [ °
].
- Para o cálculo da Equação
de Kepler, é obrigatório o emprego de M em [ radianos ],
e o valor de E obtido também está em radianos. Se é
desejado se pode converter E para [°] e
calcular os valores de seno, coseno e tangente; entretanto se E não
estiver dentro de uma função trigonométrica, então
E deverá ser tomada em radianos!
- Se a última passagem pelo periélio ocorreu há
mais de um período do planeta, então o cômputo da anomalia
média certamente dará um valor superior a 360°
ou 2p
radianos (6.2831853...). Neste caso é melhor reduzirmos a anomalia mé
dia para o valor fracionário de um giro completo. Expressando M em
radianos ou graus sexagesimais, esto se reduz à seguinte fórmula:
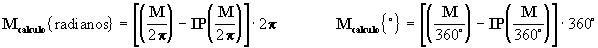
onde IP representa a função que nos dá
a parte inteira do argumento contido.
Vejamos um exemplo:
Se
M = 9.28 radianos = 531°
.7048339, então
Mcálculo{rad} = [ (9.28/2p
) - IP(9.28/2p)]2p
= [1.4769579 - 1]2p
=
= [0.4769579]2
p = 2.9968147 rad
Mcálculo {
°} = [ (531°
.7048339/360°) - IP(531.7048339/360
°)]360°
= [ 1.4769579 - 1]360°
=
= [0.4769579] 360
° = 171°
.7048339
- logo é evidente que 2.9968147 radianos = 171
°.7048339
7.
CONSIDERAÇÕES SOBRE A CONSTANTE DE GAUSS, O MOVIMENTO DIURNO
MÉDIO E A FÓRMULA DE KEPLER
- CONSTANTE DE GAUSS E MOVIMENTO DIURNO
MÉDIO
Dada a equação [14] :
 , e como:
, e como:
M = E - sen(E) =
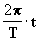
Aelipse = p
ab = p
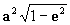
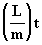 = 2At
(sendo At a área varrida até o
instante t )
= 2At
(sendo At a área varrida até o
instante t )
resulta que a equação
[14] eqüivale a:
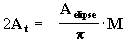 [20a]
[20a]
que encontramos foi a
expressão do dobro da área orbital varrida em um tempo t
desde o periélio. Por outro lado, se na eq. [20a] isolamos M
obtemos a eq. [20aa], logo podemos derivar a eq. [20aa]:
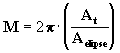 [20aa]
Þ
[20aa]
Þ [20aaa]
[20aaa]
Prestando
atenção na equação [20aa] vemos que o quociente
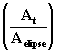 não é outra coisa
senão a expressão em forma de % da área varrida respeito
da área total; porém, M é um ângulo dependente
dp tempo t, de forma que o produto 2p
.% dá um ângulo proporcional à área varrida, ou seja ao
tempo t. Isto faz pensar num movimento circular. Na eq. [20aaa] verificamos
a proporcionalidade entre o tempo t do movimento circular e a área
varrida At (pois a velocidade angular é constante na
circunferência), ou seja, se falamos de um setor circular varrido em um
tempo t igual a 25% do período T obtemos 25% da
área do círculo, então o ângulo do setor será
25%.2p
= p/4 radianos ou 25%.360
° = 90°
. Estas considerações levam a pensar que talvez M esteja
relacionado com algum tipo de circunferência auxiliar; ou seja, a
órbita e circular e a velocidade angular é constante. Quando
tratarmos da Equação de Kepler veremos que esta idéia
é absolutamente válida.
não é outra coisa
senão a expressão em forma de % da área varrida respeito
da área total; porém, M é um ângulo dependente
dp tempo t, de forma que o produto 2p
.% dá um ângulo proporcional à área varrida, ou seja ao
tempo t. Isto faz pensar num movimento circular. Na eq. [20aaa] verificamos
a proporcionalidade entre o tempo t do movimento circular e a área
varrida At (pois a velocidade angular é constante na
circunferência), ou seja, se falamos de um setor circular varrido em um
tempo t igual a 25% do período T obtemos 25% da
área do círculo, então o ângulo do setor será
25%.2p
= p/4 radianos ou 25%.360
° = 90°
. Estas considerações levam a pensar que talvez M esteja
relacionado com algum tipo de circunferência auxiliar; ou seja, a
órbita e circular e a velocidade angular é constante. Quando
tratarmos da Equação de Kepler veremos que esta idéia
é absolutamente válida.
Analisemos agora as dimensões da constante
L/m. O momento da quantidade de movimento [L] tem
a dimensão {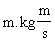 }, a
massa [m] ={
}, a
massa [m] ={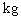 }, de forma que a
dimensão do quociente {L/m} é {m2/s}, que
multiplicado pelo tempo t nos dá uma superfície. Isto resulta
bastante claro se observamos o membro direito da equação [14], onde o
único fator não adimensional é o semi-eixo maior da órbita
a elevado ao quadrado. Ë claro que pouco interessa se a está
em metros ou unidades astronômicas, a superfície será sempre
{m2} ou {ua2}.
}, de forma que a
dimensão do quociente {L/m} é {m2/s}, que
multiplicado pelo tempo t nos dá uma superfície. Isto resulta
bastante claro se observamos o membro direito da equação [14], onde o
único fator não adimensional é o semi-eixo maior da órbita
a elevado ao quadrado. Ë claro que pouco interessa se a está
em metros ou unidades astronômicas, a superfície será sempre
{m2} ou {ua2}.
Examinando agora a equação de
Kepler, seja na sua forma dada pela equação [17], segundo a qual:
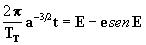 , ou na sua forma dada
pela equação [20], segundo a qual: M = E - sen
(E) , vemos que não existe fator dimensional, exceto o valor 2
p
, que está expressado em radianos, ou como já vimos antes, em graus
sexagesimais (não esquecer que para operar no lado direito da expressão
devemos trabalhar em radianos!).
, ou na sua forma dada
pela equação [20], segundo a qual: M = E - sen
(E) , vemos que não existe fator dimensional, exceto o valor 2
p
, que está expressado em radianos, ou como já vimos antes, em graus
sexagesimais (não esquecer que para operar no lado direito da expressão
devemos trabalhar em radianos!).
Ë interessante entender o que significa a constante de
Gauss:
Vamos igualar a eq. [14]:
 , com a [20]: n
Dt = E - sen(E), para
isto tomamos a eq. [14] e isolamos E - sen(E), de modo que
agora temos:
, com a [20]: n
Dt = E - sen(E), para
isto tomamos a eq. [14] e isolamos E - sen(E), de modo que
agora temos:
E - sen(E) = 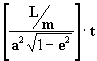
comparando esta última com a eq. [20] chegamos a:

ou seja:
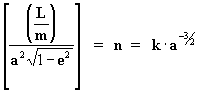 [21]
[21]
porém da eq. [8 a]:  deduzimos que :
deduzimos que :
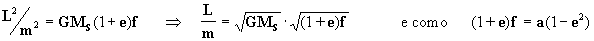
então:
 , de forma que introduzindo este valor
na equação [21] temos:
, de forma que introduzindo este valor
na equação [21] temos:
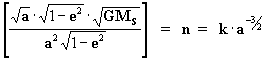
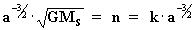 [22]
[22]
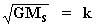 [23]
[23]
por outro lado, da equação [10]:
 de forma que temos:
de forma que temos:
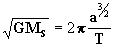 , portanto a
equação [22] do movimento diurno médio fica
da seguinte forma:
, portanto a
equação [22] do movimento diurno médio fica
da seguinte forma:

ou seja: 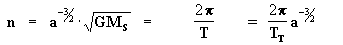 [24]
[24]
do qual:
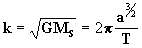 [25]
[25]
portanto, uma maneira de encontrar k e utilizar os
valores de a e T terrestres, de forma que se a = 1 ua, e T =
TT, (atenção que para qualquer outro planeta, k
se calcula pela [25]),então:
 [26]
[26]
tal como foi feito na [18a] quando introduzimos a constante de
Gauss.
Calculemos então o valor de k segundo a eq. [23],
para isto devemos passar as unidades de [G]
= {
 } para {
} para {
 }, ou seja que se G [
}, ou seja que se G [
 ] = 6.67 10-11
] = 6.67 10-11
 então:
então:
G [
 ] = 6.67 10-11
] = 6.67 10-11
 (1ua/1.495979 1011 m)
3 (86400 s/dia)2 =
(1ua/1.495979 1011 m)
3 (86400 s/dia)2 =
G [
 ] = 1.4872 10-34
] = 1.4872 10-34

e como MS = 1.991 1030 kg
então: Þk =
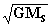 = 0.0172076
» 0.0172
= 0.0172076
» 0.0172
o que concorda com o valor introduzido pela equação
[26] pois:
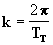 =
2p / 365.2564 dia = 0.017202
=
2p / 365.2564 dia = 0.017202
Resumindo:
- O movimento diurno médio (n)
não é senão uma expressão da velocidade angular
média do planeta (
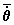 ), que resulta
de imaginar a sua órbita circular, de forma que
), que resulta
de imaginar a sua órbita circular, de forma que
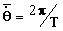 .
.
A anomalia média
(M), dá a idéia do ângulo do setor circular
varrido até o instante t, se a órbita fosse circular.
- A constante de Gauss (k) é
um valor constante para o sistema solar, portanto de igual valor para todos os planetas.
Digamos que k quantifica a "grandeza gravitacional" do sol, pois
k =
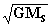
, ou seja sua capacidade
de influir gravitacionalmente sobre outras massas. Como dato interessante, esta
"grandeza gravitacional", multiplicada pela distância média
do planeta ao sol (elevada a 1.5), nos dá o movimento diurno mé
dio, ou seja como o planeta se comporta a essa distância do sol.
Quando resolvemos a equação [12], introduzimos o
parâmetro E tal que se cumpria a relação dada pela
equação [12a] :  .
Resta perguntar agora o que a eq. [12a] significa.
.
Resta perguntar agora o que a eq. [12a] significa.
Vamos dar uma olhada na Figura 6:

Nesta figura observamos o sol, dado pelo ponto S, a
posição do planeta, dado pelo ponto P, na sua órbita
elíptica de periélio SQ¸excentricidade e, e
dimensões orbitais a e b. Agora traçamos uma
órbita circular de raio a e centro O, que obviamente
não coincide com S, nesta órbita circular temos um planeta
imaginário, de idênticas caraterísticas a P, denominado
P’. Este planeta P’ tem o mesmo período orbital T que
P porém, movimenta-se com velocidade angular uniforme (já que a
órbita é circular). Resulta evidente que a velocidade angular do planeta
P’ vale 2p
/T, mas isto não é outra coisa senão o movimento
diurno médio do planeta P.
A posição do planeta P
em coordenadas polares de centro S está definida pela anomalia
verdadeira (q
), e o raio vetor (r). A posição do planeta
P em coordenadas polares de centro O(excêntrico respeito de
S) está definida pela anomalia
excêntrica (E), e o raio vetor
(a).
Vamos demonstrar agora a correspondência
entre as posições de P e P’ tal como mostradas na Figura 6.
Analisando a figura observamos que a componente horizontal do raio vetor a de
P’, vale acosE. Este valor é igual à
distância c + x, mas c = ae, e x = rcos
q. Lembrando que r vale
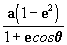 (elipse com o centro de coordenadas
polares centrado no foco direito), então podemos dizer que:
(elipse com o centro de coordenadas
polares centrado no foco direito), então podemos dizer que:
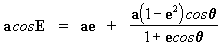 . Após operarmos nesta
igualdade podemos encontrar o valor de cosE, ou seja:
. Após operarmos nesta
igualdade podemos encontrar o valor de cosE, ou seja:
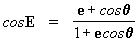 [27]
[27]
Lembrando das
funções trigonométricas que
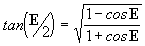 , podemos introduzir a
equação [27] nesta última, de forma que:
, podemos introduzir a
equação [27] nesta última, de forma que:
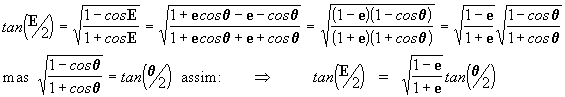
que é precisamente a equação [12a], tal
como queríamos demonstrar. Agora sabemos o real significado do conceito
anomalia excêntrica.
8. CÁLCULO DE ÓRBITAS NÃO ELÍPTICAS: ÓRBITAS
PARABÓLICAS E HIPERBÓLICAS
- CÁLCULO DAS ÓRBITAS
PARABÓLICAS
Quando chegamos à equação [8aa] que nos
dava a fórmula geral da cônica, continuamos nosso raciocínio
assumindo que 0 < e < 1, logo, para chegar até a
equação de Kepler, introduzimos o valor de r n? cálculo
da integral dada pela equação [11]. Para o caso das órbitas
parabólicas, sabemos que e = 1, porém vamos refazer a
integração da [11] considerando a equação da
parábola (que resulta de introduzir e=1 na eq. [8aa]).
Vejamos a Figura 7: a distância focal
SQ do sol à passagem pelo periélio, foi chamada de f;
a excentricidade da elipse vale e = 1, assim colocando estes
dados na equação [8aa]:  ,
chegamos a equação da órbita parabólica:
,
chegamos a equação da órbita parabólica:
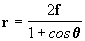 . Agora, apenas por uma questão
de nomenclatura, denominamos à distância focal f de q,
ou seja q = f.
. Agora, apenas por uma questão
de nomenclatura, denominamos à distância focal f de q,
ou seja q = f.
Portanto a equação da parábola é:
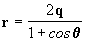 [28]
[28]
Agora vamos
fazer a integração: 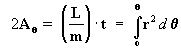 ,
introduzindo o valor de r dado pela eq. [28].
,
introduzindo o valor de r dado pela eq. [28].
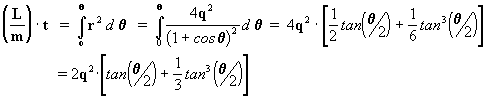
porém como
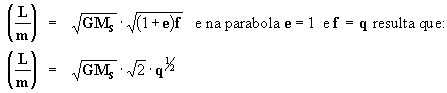
então:

isolando agora o termo das tangentes:
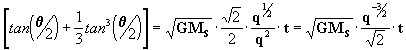
ou seja que:
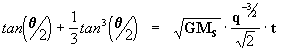 [29]
[29]
equação análoga a
[17] no sentido que na sua resolução obtemos o valor de
q.
Neste caso temos que resolver uma equação
cúbica em tan(q/2). Pode-se demonstrar
que esta equação tem uma raiz real (a que nos interessa) e duas
imaginárias. Existem bastantes métodos de resolução.
Propomos o Método de Newton, que diz: Se x0
é um valor aproximado da raiz da função
f(x)=0 então como aproximação mais exata se
toma
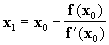 Substituindo agora x1 por x0 obtemos
uma melhor aproximação x2.
Substituindo agora x1 por x0 obtemos
uma melhor aproximação x2.
Logo,
para nosso problema (resolução da equação [29]):
- Para facilitar os cálculos:
multiplicamos a eq. [29] por três e chamamos a tan(
q/2) = E, ou seja a equação
[29] passa agora a ser: E3 + 3E - M = 0
- definimos M = n .t, onde n
=
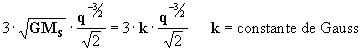
- aplicamos o método de Newton, de forma que denominando
E0 ao valor aproximado da raiz, o próximo valor será:
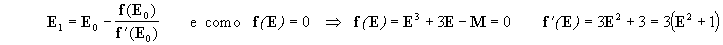
logo: 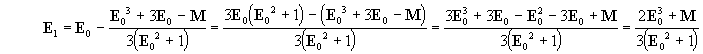
ou seja
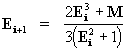 [29a]
[29a]
Este valor será iterado até que f( Ei )
» 0 , por exemplo até que
½ f( Ei ) ½
=
10-8.
- A primeira
aproximação, isto é E0 , vale
E0 = 0
- iteramos então de acordo ao seguinte algoritmo em QBASIC da Microsoft:
10 M = nt
20 E = 0
30 E1 = 2E3 + M / [3(E2 + 1)]
40 IF ½
E1 3 + 3E1 - M
½ > 10-8 THEN
50 E = E1 : GOTO 30
60 END IF
70 q = 2 . Atan ( E )
- CÁLCULO DAS
ÓRBITAS HIPERBÓLICAS
Neste caso se procede como no anterior, lembrando que se e
> 1 então  pois segundo a
definição na hipérbole, c > a Þ
f = c - a Þ
(1+e)f = (1+e)(e-1)a = a(e2-1), logo:
pois segundo a
definição na hipérbole, c > a Þ
f = c - a Þ
(1+e)f = (1+e)(e-1)a = a(e2-1), logo:

então:
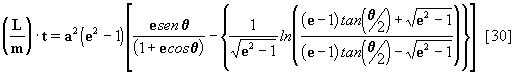
Vamos agora fazer algumas considerações a
respeito das funções trigonométricas hiperbólicas,
para isto tomamos o fator dentro do logaritmo natural na equação
[30]:
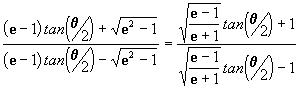 e se
e se

então temos que:
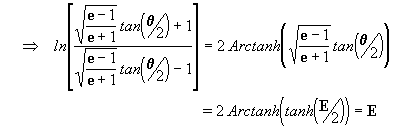
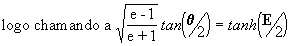
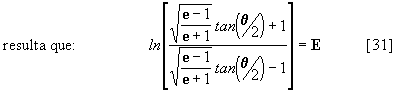
podemos agora calcular o valor de
senh(E), ou seja:

logo se deduz que
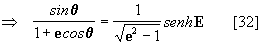
assim, introduzindo as
equações [31] e [32] na equação [30] obtemos:
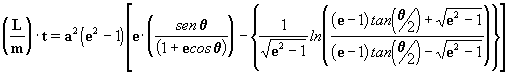
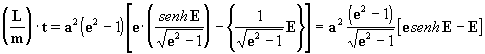
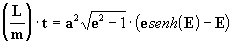 [33]
[33]
lembrando agora que na equação geral
das cônicas [8], o numerador representa o parâmetro p que
vale (1+e)f, então, de acordo com a eq. [8a] obtemos, como
principio geral para as órbitas cônicas:

porém na
definição inicial de hipérbole tínhamos visto que
 , ou seja que:
, ou seja que:
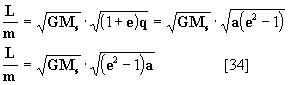
de forma que
introduzindo a eq. [34] na equação [33]:
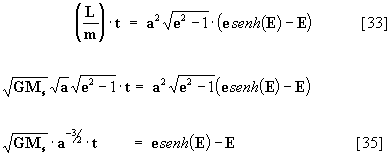

e como a = q / (e-1) para a hipérbole,
então a eq. [35]:
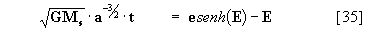
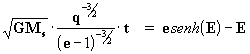 [36]
[36]
Equação parecida
a obtida no cálculo das órbitas elípticas, neste caso a
resolução da eq. [36] é idêntico ao da equação
[17] ou [20], ou seja:
E = e
senh(E) - M
M = n.t
n =  onde
onde
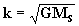

 com origem num centro O de coordenadas ortogonais retangulares.
Definindo nesta terna xyz,
os versores (vetores unitários) dos eixos, obtemos
respectivamente : o versor
com origem num centro O de coordenadas ortogonais retangulares.
Definindo nesta terna xyz,
os versores (vetores unitários) dos eixos, obtemos
respectivamente : o versor  como versor da
direção x, o versor
como versor da
direção x, o versor  como o versor da direção y, e o versor
como o versor da direção y, e o versor
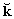 como o versor da direção z.
Assim, qualquer vetor definido num destes eixos estará representado pelo produto
de um escalar igual ao módulo e do versor da direção
como o versor da direção z.
Assim, qualquer vetor definido num destes eixos estará representado pelo produto
de um escalar igual ao módulo e do versor da direção .
.


 tal que
tal que
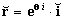 onde
onde  , logo:
, logo:
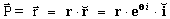

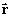 , ou seja
, ou seja
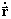 :
: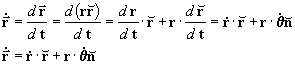
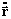 :
: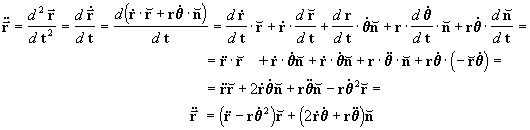


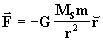

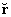 é o versor (vetor unitário)
da direção de
é o versor (vetor unitário)
da direção de
 e:
e: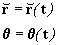

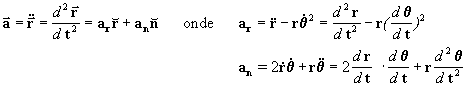
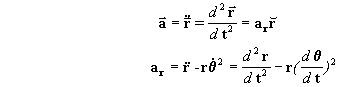
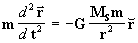
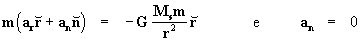

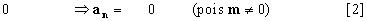
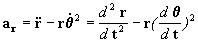
 , mas lembrando da equaçã
o [2] obtemos que:
, mas lembrando da equaçã
o [2] obtemos que:
 entretanto
entretanto
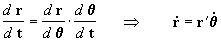
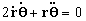 podemos obter
podemos obter
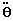 , ou seja:
, ou seja: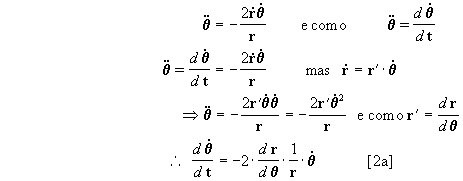

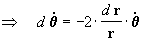

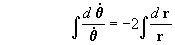
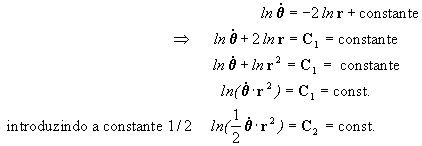
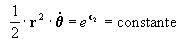

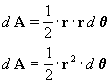

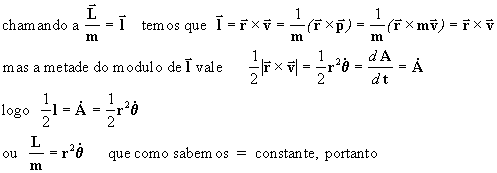

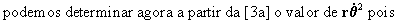
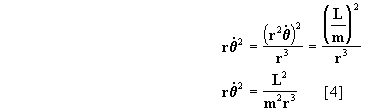
 porém falta conhecermos o valor de
porém falta conhecermos o valor de
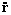 . Para isto, e voltando agora
à aceleração radial:
. Para isto, e voltando agora
à aceleração radial:
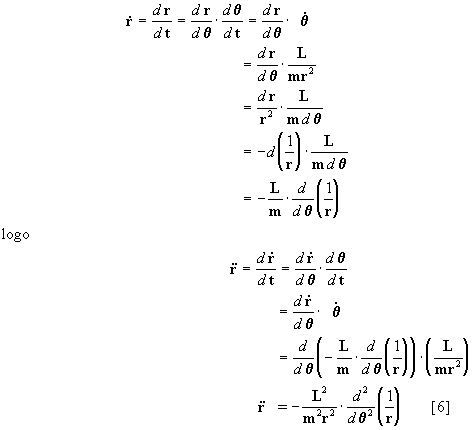
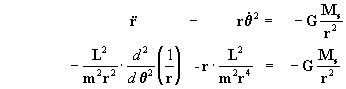
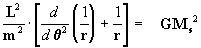
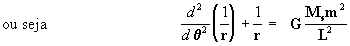
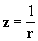 e
substituindo, chegamos a uma equação diferencial [7] de
fácil resolução:
e
substituindo, chegamos a uma equação diferencial [7] de
fácil resolução: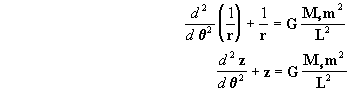
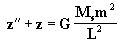
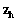 que provém de resolver
que provém de resolver
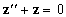 , e a solução particular
, e a solução particular
 .
.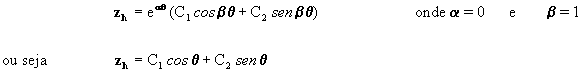
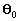 e
e
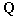 de forma que:
de forma que: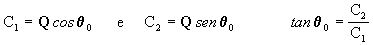


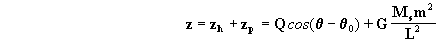
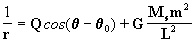
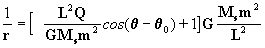
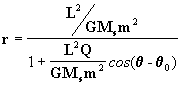

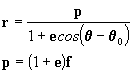 [8aa]
[8aa] [8 a]
[8 a]
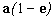

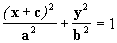
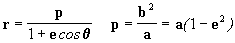
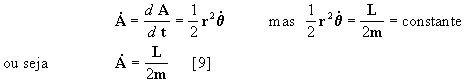
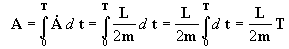
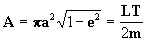
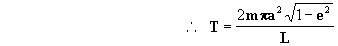
 , ou seja:
, ou seja: [10]
[10]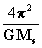 é uma constante para todos os
planetas do sistema solar. Assim temos que
é uma constante para todos os
planetas do sistema solar. Assim temos que 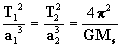 onde os subíndices 1,2, representam os diferentes planetas.
Tal é a 3a. Lei de Kepler: "Os quadrados dos períodos
de revolução dos planetas são inversamente proporcionais às
distâncias medias do sol".
onde os subíndices 1,2, representam os diferentes planetas.
Tal é a 3a. Lei de Kepler: "Os quadrados dos períodos
de revolução dos planetas são inversamente proporcionais às
distâncias medias do sol".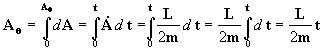
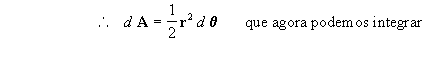
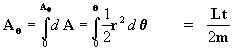 [11]
[11] 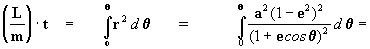
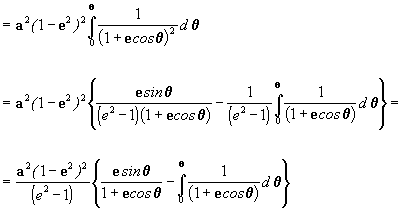
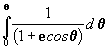 será:
será: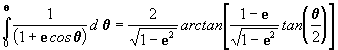
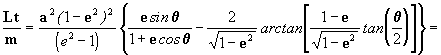
 [12]
[12]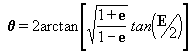
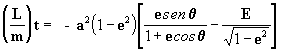 [13]
[13]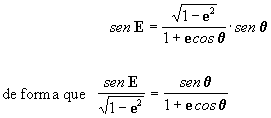
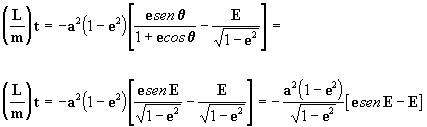
 [14]
[14] [15]
[15]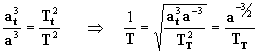 [16]
[16]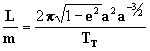
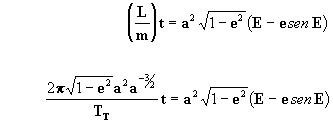
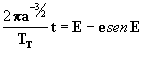 [17]
[17]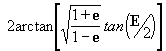 [18]
[18]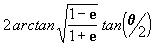 [radianos]
[radianos]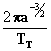 [radianos/dia]
[radianos/dia]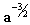 onde k=constante de Gauss =
onde k=constante de Gauss =
 [18a]
[18a]
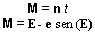


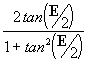 =-0.584818898 Þ
<0 Þ estamos no IV quadrante!
=-0.584818898 Þ
<0 Þ estamos no IV quadrante!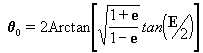 = -0.654082984
= -0.654082984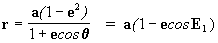 = 4.999964739 ua
= 4.999964739 ua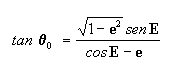 retorna o argumento q
no seu valor principal, ou seja q
0, no I e IV quadrantes.
retorna o argumento q
no seu valor principal, ou seja q
0, no I e IV quadrantes.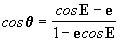
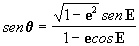
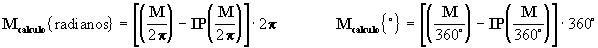
 , e como:
, e como: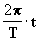
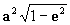
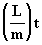 = 2At
(sendo At a área varrida até o
instante t )
= 2At
(sendo At a área varrida até o
instante t )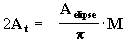 [20a]
[20a] 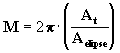 [20aa]
Þ
[20aa]
Þ [20aaa]
[20aaa]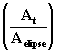 não é outra coisa
senão a expressão em forma de % da área varrida respeito
da área total; porém, M é um ângulo dependente
dp tempo t, de forma que o produto 2p
.% dá um ângulo proporcional à área varrida, ou seja ao
tempo t. Isto faz pensar num movimento circular. Na eq. [20aaa] verificamos
a proporcionalidade entre o tempo t do movimento circular e a área
varrida At (pois a velocidade angular é constante na
circunferência), ou seja, se falamos de um setor circular varrido em um
tempo t igual a 25% do período T obtemos 25% da
área do círculo, então o ângulo do setor será
25%.2p
= p/4 radianos ou 25%.360
° = 90°
. Estas considerações levam a pensar que talvez M esteja
relacionado com algum tipo de circunferência auxiliar; ou seja, a
órbita e circular e a velocidade angular é constante. Quando
tratarmos da Equação de Kepler veremos que esta idéia
é absolutamente válida.
não é outra coisa
senão a expressão em forma de % da área varrida respeito
da área total; porém, M é um ângulo dependente
dp tempo t, de forma que o produto 2p
.% dá um ângulo proporcional à área varrida, ou seja ao
tempo t. Isto faz pensar num movimento circular. Na eq. [20aaa] verificamos
a proporcionalidade entre o tempo t do movimento circular e a área
varrida At (pois a velocidade angular é constante na
circunferência), ou seja, se falamos de um setor circular varrido em um
tempo t igual a 25% do período T obtemos 25% da
área do círculo, então o ângulo do setor será
25%.2p
= p/4 radianos ou 25%.360
° = 90°
. Estas considerações levam a pensar que talvez M esteja
relacionado com algum tipo de circunferência auxiliar; ou seja, a
órbita e circular e a velocidade angular é constante. Quando
tratarmos da Equação de Kepler veremos que esta idéia
é absolutamente válida.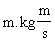 }, a
massa [m] ={
}, a
massa [m] ={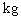 }, de forma que a
dimensão do quociente {L/m} é {m2/s}, que
multiplicado pelo tempo t nos dá uma superfície. Isto resulta
bastante claro se observamos o membro direito da equação [14], onde o
único fator não adimensional é o semi-eixo maior da órbita
a elevado ao quadrado. Ë claro que pouco interessa se a está
em metros ou unidades astronômicas, a superfície será sempre
{m2} ou {ua2}.
}, de forma que a
dimensão do quociente {L/m} é {m2/s}, que
multiplicado pelo tempo t nos dá uma superfície. Isto resulta
bastante claro se observamos o membro direito da equação [14], onde o
único fator não adimensional é o semi-eixo maior da órbita
a elevado ao quadrado. Ë claro que pouco interessa se a está
em metros ou unidades astronômicas, a superfície será sempre
{m2} ou {ua2}.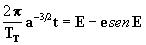 , ou na sua forma dada
pela equação [20], segundo a qual: M = E - sen
(E) , vemos que não existe fator dimensional, exceto o valor 2
p
, que está expressado em radianos, ou como já vimos antes, em graus
sexagesimais (não esquecer que para operar no lado direito da expressão
devemos trabalhar em radianos!).
, ou na sua forma dada
pela equação [20], segundo a qual: M = E - sen
(E) , vemos que não existe fator dimensional, exceto o valor 2
p
, que está expressado em radianos, ou como já vimos antes, em graus
sexagesimais (não esquecer que para operar no lado direito da expressão
devemos trabalhar em radianos!).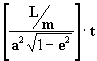

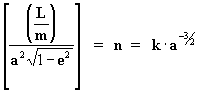 [21]
[21] deduzimos que :
deduzimos que : 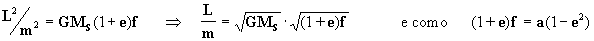
 , de forma que introduzindo este valor
na equação [21] temos:
, de forma que introduzindo este valor
na equação [21] temos: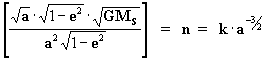
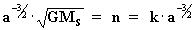 [22]
[22]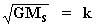 [23]
[23]
 de forma que temos:
de forma que temos: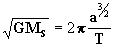 , portanto a
equação [22] do movimento diurno médio fica
da seguinte forma:
, portanto a
equação [22] do movimento diurno médio fica
da seguinte forma:
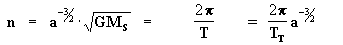 [24]
[24]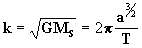 [25]
[25] [26]
[26]
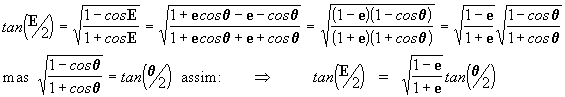
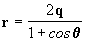 [28]
[28]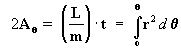 ,
introduzindo o valor de r dado pela eq. [28].
,
introduzindo o valor de r dado pela eq. [28].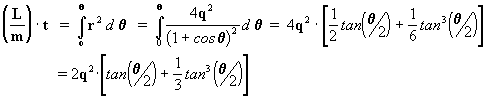
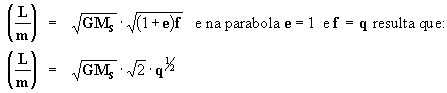

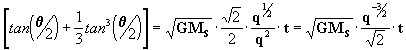
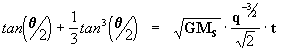 [29]
[29]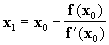 Substituindo agora x1 por x0 obtemos
uma melhor aproximação x2.
Substituindo agora x1 por x0 obtemos
uma melhor aproximação x2.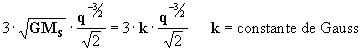
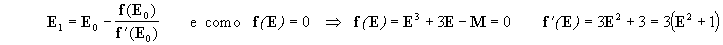
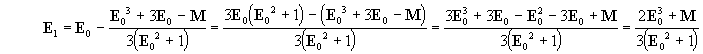
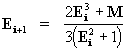 [29a]
[29a] pois segundo a
definição na hipérbole, c > a Þ
f = c - a Þ
(1+e)f = (1+e)(e-1)a = a(e2-1), logo:
pois segundo a
definição na hipérbole, c > a Þ
f = c - a Þ
(1+e)f = (1+e)(e-1)a = a(e2-1), logo:
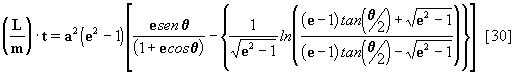
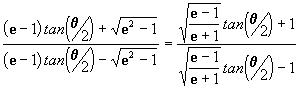 e se
e se

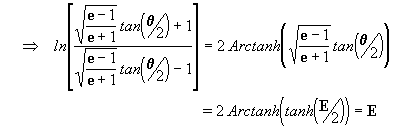
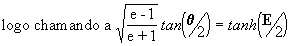
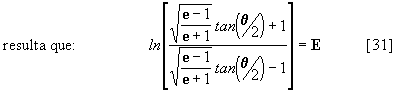

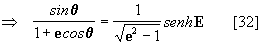
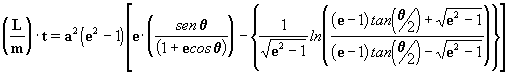
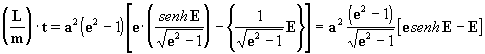
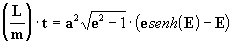 [33]
[33]
 , ou seja que:
, ou seja que:
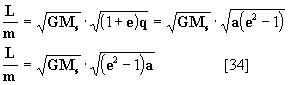
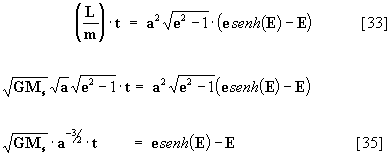
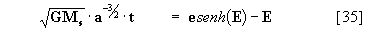
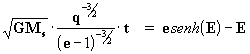 [36]
[36] onde
onde