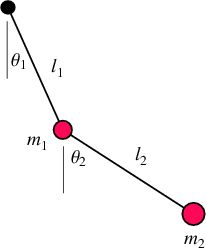
A double pendulum consists of one pendulum attached to another. Double pendula are an example of a simple physical system which can exhibit chaotic behavior. Consider a double bob pendulum with masses and attached by rigid massless wires of lengths and . Further, let the angles the two wires make with the vertical be denoted and , as illustrated above. Finally, let gravity be given by g. Then the positions of the bobs are given by

			(5)
			(6)

			(7)
			(8)

The Lagrangian is then

	(9)

Therefore, for ,

			(10)
			(11)
			(12)

so the Euler-Lagrange differential equation for becomes

	(13)

Dividing through by , this simplifies to

	(14)

Similarly, for ,

			(15)
			(16)
			(17)

so the Euler-Lagrange differential equation for becomes

(18)

Dividing through by , this simplifies to

(19)

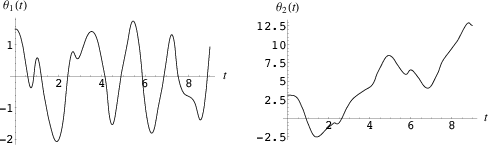
The coupled second-order ordinary differential equations (14) and (19) can be solved numerically for and , as illustrated above for one particular choice of parameters and initial conditions. Plotting the resulting solutions quickly reveals the complicated motion.

The equations of motion can also be written in the Hamiltonian formalism. Computing the generalized momenta gives

			(20)
			(21)

The Hamiltonian is then given by

	(22)

Solving (20) and (21) for and and plugging back in to (22) and simplifying gives

	(23)

This leads to the Hamilton's equations

			(24)
			(25)
			(26)
			(27)

where

(28)

and

(29)

Coupled Pendula, Hamiltonian, Lagrangian, Pendulum