4^a Lista de Exercícios
Livro texto : Marion Thornton, 4^a ediçao.
Capítulo 7 - Formalismo Lagrangeano

Exercícios : 7 - 3, 7 - 4, 7 - 6, 7 - 7, 7 - 12, 7 - 14 e 7 - 16.

1 - A energia cinética de uma particula de massa m é dada por 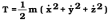. Partindo das equações de transformações de coordenadas:      a) cilíndricas x=r cosθ, y=r senθ e z=z      b) esféricas x=r senθ cosφ, y=r senθ senφ e z=r cosθ e derivando em relação ao tempo, obtenha a expressão para a energia cinética da partícula em cada um destes sistemas de coordenadas.

2 - Escreva a lagrangeana para um ioio de massa m e momento de inércia I e obtenha as equações de movimento.

	3 - A bolinha da figura tem raio b e massa m e rola sem deslizar na superfície da esféra de raio a até escapar. Para este movimento, determine :      (a) o número de graus de liberdade do movimento ?      (b) a lagrangeana para a bolinha.      (c) a equação do movimento e a equação da velocidade angular, em função do tempo, para a bolinha.

4 - Um corpo de massa m está sobre um plano que gira com velocidade angular ω em torno de uma de reta horizontal, no campo gravitacional. No instante inicial o plano é está na horizontal.      (a) o número de graus de liberdade do sistema;      (b) a lagrangeana para o sistema;      (c) as equações do movimento.

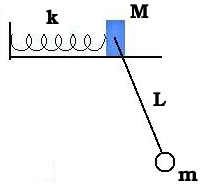5 - Um bloco de massa M está preso numa das extremidades de uma mola de constante elástica k. A outra extremidade da mola está presa a uma parede vertical. Um pêndulo de comprimento L e massa m está preso no centro do bloco, como mostra a figura. Coloque o sistema de coordenadas no ponto de equilíbrio da mola e determine:      (a) o número de graus de liberdade do sistema;      (b) a lagrangeana para o sistema;      (c) as equações do movimento.

Voltar a página principal